Humidité relative : Faire la moyenne, ou ne pas faire la moyenne ?

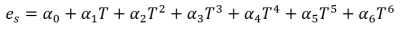
où T est la température en Celsius et les valeurs des coefficients ajustés (α) sont les suivantes :

Bien qu'il existe d'autres méthodes pour obtenir la pression de vapeur de saturation que nous pourrions envisager, le modèle de Lowe est utilisé dans les centrales de mesure de Campbell Scientific, je limiterai donc ma discussion à cette méthode pour les besoins de cet article.

Il y a deux raisons pour lesquelles une simple moyenne de l'humidité relative sur un intervalle de données donné n'est généralement pas la meilleure pratique. Premièrement, l'HR est une valeur calculée. Les mathématiciens et les statisticiens nous conseillent d'utiliser les données originales dans des opérations telles que les moyennes, puis de calculer la valeur souhaitée. En outre, l'HR est, par définition, limitée aux valeurs comprises entre zéro et 100. Par conséquent, les valeurs proches de ces limites supérieures et inférieures ne peuvent pas varier autant que celles qui se situent vers le milieu, ce qui est contraire aux hypothèses statistiques.

La deuxième raison, plus importante encore, de ne pas utiliser de moyenne simple pour l'humidité relative est que la valeur peut changer rapidement avec la température, en particulier à des températures plus élevées. La figure 1 montre la relation entre la température et la pression de vapeur de saturation sur la base du modèle de Lowe.

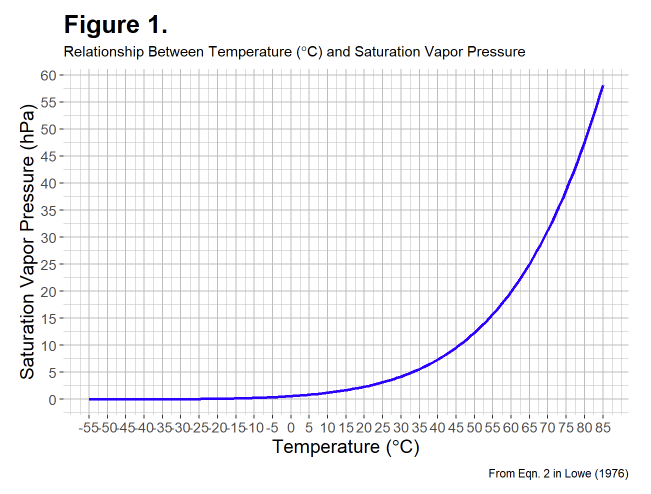
Il faut noter en particulier que la pression de vapeur de saturation change plus rapidement à des températures plus élevées. Par conséquent, les moyennes arithmétiques simples de l'humidité relative à des températures plus élevées sont susceptibles d'avoir une plus grande erreur. L'établissement de moyennes sur des intervalles plus longs est également susceptible d'entraîner une erreur plus importante.

Comment calculer correctement la moyenne de l'HR

La méthode préférée pour obtenir un HR moyen sur un intervalle donné consiste à faire la moyenne des pressions de vapeur et des pressions de vapeur de saturation, puis à calculer le HR à partir de ces moyennes. Voici un lien pour télécharger un programme CRBasic qui fait exactement cela. Lors de chaque analyse, ce programme calcule la pression de vapeur et la pression de vapeur à saturation, puis stocke les moyennes de pression de vapeur dans un tableau temporaire et caché. Ces valeurs sont ensuite utilisées pour calculer l'HR, et toutes les valeurs sont stockées dans le tableau horaire principal.

Pour illustrer la différence entre les deux méthodes de calcul d'une moyenne pour l'humidité relative (arithmétique simple par rapport à la pression de vapeur moyenne), j'ai recueilli des données d'une station météorologique près des installations de Campbell Scientific à Logan, dans l'Utah, pendant environ 17 mois. Un programme similaire à celui décrit ci-dessus a été utilisé, et les données ont été stockées à quatre intervalles :

• 30 minutes
• 1 heure
• 3 heures
• 24 heures

La figure 2 présente les résultats :

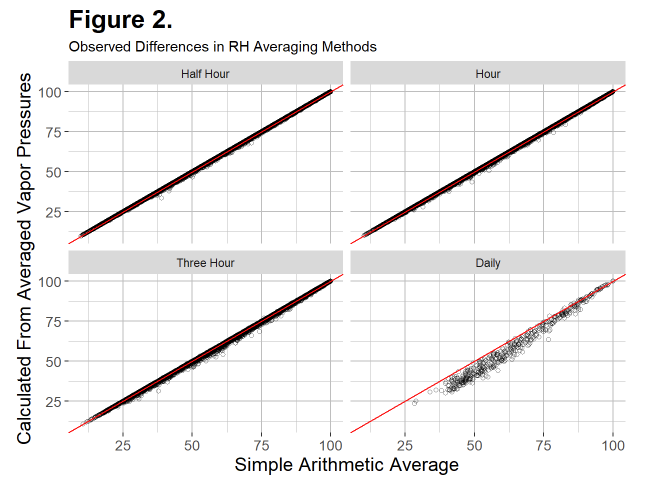
Si les deux méthodes étaient identiques, nous nous attendrions à ce que tous les points de données soient alignés sur les lignes rouges 1:1. Pour les intervalles d'une demi-heure et d'une heure, il y a un bon accord. Toutefois, pour les intervalles plus longs, l'erreur augmente considérablement. Il est intéressant de noter que, du moins pour ces données, l'erreur due à la simple moyenne se traduit presque toujours par un biais positif. En d'autres termes, une moyenne arithmétique simple surestime presque toujours l'humidité relative moyenne.

L'Organisation météorologique mondiale (OMM)2 et l'American Association of State Climatologists (AASC) recommandent toutes deux que l'incertitude (erreur) de la mesure de l'humidité relative soit inférieure à 3 %. Dans le pire des cas, l'erreur due au calcul de la moyenne de l'HR s'ajouterait à l'erreur du capteur. Par exemple, si les spécifications d'un capteur indiquent qu'il se situe à 2,3% sur la majeure partie de la plage, toute erreur supplémentaire devrait être limitée à moins de 1% pour respecter, de manière prudente, les recommandations de l'OMM et de l'AASC.

Le tableau 1 présente quelques statistiques concernant la différence entre les méthodes de calcul de la moyenne (moyenne simple moins la moyenne de la pression de vapeur), y compris la moyenne, le maximum et le minimum, ainsi que quelques percentiles. Cinquante pour cent des données se situent entre les 25 et 75 percentiles, et 95 % des données se situent entre les 2,5 et 97,5 percentiles.

Table 1. Comparaison de la différence entre la moyenne simple et la moyenne des pressions de vapeur

Pour les intervalles d'une demi-heure et d'une heure, la plupart des données se situent à moins de 1 % l'une de l'autre. Par conséquent, des moyennes simples peuvent être acceptables pour ces intervalles, selon le capteur utilisé et l'objectif des données, entre autres considérations. Cependant, des intervalles plus longs présentent un biais important et démontrent qu'une simple moyenne de l'humidité relative ne représenterait pas bien les données. En outre, il est à noter qu'il pourrait être plus instructif pour de nombreuses données de stocker d'autres mesures telles que le point de rosée ou, simplement, la pression de vapeur. 

J'espère que cela permettra de clarifier les raisons pour lesquelles il n'est généralement pas judicieux de faire une moyenne de l'humidité relative pour des raisons mathématiques et statistiques, mais aussi pragmatiques. Si vous avez vraiment besoin d'une humidité relative moyenne, en particulier sur de longs intervalles de temps, la meilleure pratique consiste à utiliser la moyenne observée et les pressions de vapeur de saturation pour calculer l'humidité relative sur chaque intervalle de temps. Vous pouvez modifier ce programme en exemple téléchargeable selon vos besoins. Sinon, il suffit de stocker la pression de vapeur et la température observées (facilement réalisable dans une centrale d'acquisition de mesure de Campbell Scientific). A partir de ces données, l'humidité relative et le point de rosée peuvent être calculés en post-traitement si nécessaire.

Si vous avez des questions sur le calcul de la moyenne de l'humidité relative (HR), veuillez les poster ci-dessous..